गॉस का नियम क्या है?

मैक्सवेल के विद्युत चुंबकत्व के चार मूल समीकरणों में गॉस का नियम एक अत्यंत महत्वपूर्ण नियम है। यह नियम विद्युत क्षेत्र (Electric Field) और विद्युत आवेश (Electric Charge) के बीच संबंध को स्पष्ट करता है। इस नियम का प्रतिपादन प्रसिद्ध गणितज्ञ एवं भौतिक विज्ञानी कार्ल फ्रेडरिक गॉस द्वारा वर्ष 1835 में किया गया था।
गॉस का नियम यह बताता है कि किसी बंद सतह (Closed Surface) से होकर गुजरने वाला कुल वैद्युत फ्लक्स उस सतह के भीतर स्थित कुल विद्युत आवेश पर निर्भर करता है, न कि सतह के आकार या आकृति पर।

गॉस का नियम

गॉस के नियम के अनुसार, किसी बंद पृष्ठ से गुजरने वाला कुल वैद्युत फ्लक्स उसके अंदर उपस्थित कुल विद्युत आवेश का 1/ε₀ गुना होता है।

जहां ε₀ (एप्सिलॉन नॉट) निर्वात अथवा वायु की विद्युतशीलता (Permittivity of Free Space) है ।
उदाहरण के लिए,
एक बिंदु आवेश q को किनारे ‘a’ के घन के अंदर रखा गया है। अब गॉस नियम के अनुसार, घन के प्रत्येक फलक से गुजरने वाला फ्लक्स q/6ε₀है।
विद्युत क्षेत्र बिजली के बारे में जानने की मूल अवधारणा है। आमतौर पर, सतह के विद्युत क्षेत्र की गणना कूलम्ब के नियम को लागू करके की जाती है, लेकिन एक बंद सतह में विद्युत क्षेत्र के वितरण की गणना करने के लिए, हमें गॉस कानून की अवधारणा को समझने की आवश्यकता है। यह एक बंद में संलग्न विद्युत आवेश या संलग्न बंद सतह में मौजूद विद्युत आवेश की व्याख्या करता है।

गॉस के नियम का सूत्र

एक बंद सतह में संलग्न कुल आवेश सतह से घिरे कुल फ्लक्स के समानुपाती होता है। इसलिए, यदि कुल फ्लक्स ϕ है और ε₀ विद्युत स्थिरांक है, तो सतह से घिरा कुल विद्युत आवेश Q है;
गॉस नियम सूत्र द्वारा व्यक्त किया जाता है,

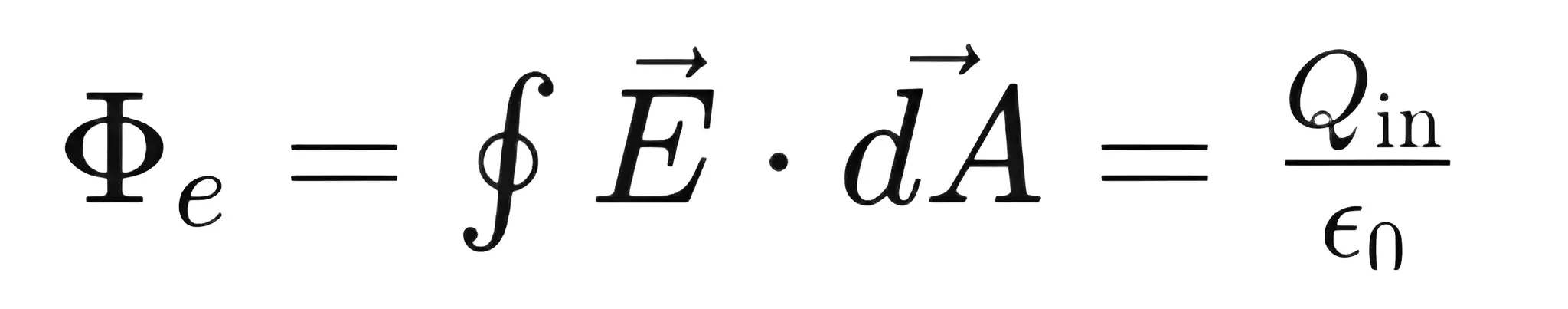
गॉस का प्रमेय

किसी बंद सतह से होकर गुजरने वाला कुल वैद्युत फ्लक्स, उस सतह के भीतर स्थित कुल आवेश के समानुपाती होता है।

यह प्रमेय विद्युत क्षेत्र रेखाओं (Electric Field Lines) के प्रवाह (Flux) और आवेश के बीच सीधा संबंध स्थापित करता है।

ϕ = Q/ε₀

• Φ (फाई) = कुल वैद्युत फ्लक्स
•  Q = बंद सतह के भीतर स्थित कुल विद्युत आवेश
•  ε₀ = निर्वात की विद्युतशीलता

सरल शब्दों में, गॉस प्रमेय विद्युत क्षेत्र रेखाओं (फ्लक्स) के ‘प्रवाह’ को संलग्न सतह के भीतर आवेशों से संबंधित करता है। यदि किसी बंद सतह के अंदर कोई आवेश नहीं है, तो उस सतह से गुजरने वाला कुल वैद्युत फ्लक्स शून्य होगा।

उदाहरण (Example)

प्रश्न: यदि किसी बिंदु आवेश q को किनारे a वाले एक घन (Cube) के केंद्र में रखा जाए, तो घन के प्रत्येक फलक से गुजरने वाला वैद्युत फ्लक्स कितना होगा?
उत्तर: घन के कुल 6 फलक होते हैं और कुल फ्लक्स = q/ε₀ अतः प्रत्येक फलक से गुजरने वाला फ्लक्स होगा q/6ε₀

गॉस के नियम के अनुप्रयोग

गॉस का नियम निम्नलिखित स्थितियों में विशेष रूप से उपयोगी है:

• अनंत लंबाई की रेखीय आवेश (Infinite Line Charge) के कारण विद्युत क्षेत्र की तीव्रता ज्ञात करने में।
• समरूप अनंत आवेशित कुचालक चादर (Infinite Charged Non-Conducting Sheet) के लिए विद्युत क्षेत्र निकालने में।
• अनंत समरूप आवेशित चालक प्लेट (Infinite Conducting Plate) के कारण उत्पन्न विद्युत क्षेत्र की गणना में।
• गोलाकार, बेलनाकार एवं समतलीय सममिति वाली समस्याओं में।

गॉस के नियम का महत्व

• यह विद्युत क्षेत्र की गणना को सरल बनाता है।
• सममित (Symmetrical) आवेश वितरण में यह कूलॉम के नियम की तुलना में अधिक उपयोगी होता है।
• यह मैक्सवेल के समीकरणों का आधार है।
• विद्युत क्षेत्र की भौतिक व्याख्या को स्पष्ट करता है।

अक्सर पूछे जाने वाले प्रश्न (FAQs)

1. गॉस का नियम क्या है?

उत्तर: गॉस का नियम बताता है कि किसी बंद सतह से होकर गुजरने वाला कुल वैद्युत फ्लक्स उस सतह के भीतर स्थित कुल विद्युत आवेश के 1/ε₀ गुना के बराबर होता है। यह नियम विद्युत क्षेत्र और आवेश के बीच संबंध को दर्शाता है।

2. गॉस का नियम किसने प्रतिपादित किया था?

उत्तर: गॉस का नियम प्रसिद्ध जर्मन वैज्ञानिक Carl Friedrich Gauss द्वारा प्रतिपादित किया गया था।

3. गॉस के नियम का सूत्र क्या है?

उत्तर: गॉस के नियम का गणितीय सूत्र है, Φ = Q/ε₀ जहाँ Φ कुल वैद्युत फ्लक्स, Q संलग्न आवेश और ε₀ निर्वात की विद्युतशीलता है।

 

4. वैद्युत फ्लक्स (Electric Flux) क्या होता है?

उत्तर: वैद्युत फ्लक्स किसी सतह से होकर गुजरने वाली विद्युत क्षेत्र रेखाओं की संख्या का माप है। यह दर्शाता है कि विद्युत क्षेत्र किसी सतह से कितनी मात्रा में गुजर रहा है।

5. यदि बंद सतह के अंदर कोई आवेश न हो तो क्या होगा?

उत्तर: यदि किसी बंद सतह के भीतर कोई विद्युत आवेश नहीं है, तो उस सतह से गुजरने वाला कुल वैद्युत फ्लक्स शून्य (0) होगा, चाहे बाहरी क्षेत्र कितना भी मजबूत क्यों न हो।

6. क्या गॉस का नियम हर स्थिति में विद्युत क्षेत्र ज्ञात करने के लिए उपयोगी है?

उत्तर: नहीं। गॉस का नियम मुख्य रूप से सममित (Symmetrical) आवेश वितरण जैसे गोलाकार, बेलनाकार या समतलीय स्थितियों में अधिक प्रभावी होता है।

7. गॉस का नियम और कूलॉम का नियम में क्या अंतर है?

उत्तर: कूलॉम का नियम व्यक्तिगत आवेशों के बीच बल की गणना करता है, जबकि गॉस का नियम पूरे आवेश वितरण और उससे उत्पन्न विद्युत क्षेत्र के फ्लक्स को समझने में मदद करता है।

8. गॉस के नियम का उपयोग कहाँ किया जाता है?

उत्तर: गॉस के नियम का उपयोग निम्न स्थितियों में किया जाता है:

• अनंत रेखीय आवेश
• अनंत आवेशित चादर
• समरूप आवेशित चालक प्लेट
• गोलाकार एवं बेलनाकार आवेश वितरण

9. ε₀ (एप्सिलॉन नॉट) का भौतिक अर्थ क्या है?

उत्तर: ε₀ निर्वात की विद्युतशीलता है, जो यह दर्शाती है कि निर्वात में विद्युत क्षेत्र कितनी आसानी से बन सकता है। यह एक स्थिरांक है जिसका मान लगभग 8.85 × 10⁻¹² C²/N·m² होता है।